Gin Rummy: The Conclusion

Gin Rummy is officially over. First, congrats to Eric for winning the in-class tournament. Each round consisted of 8 games, with the semi-finals and finals being 16 games, and the AI that achieved more points moved on. I lost in the first round.

BUT. Card games have a heavy hand in random distributions. It felt like who moved on was largely based on luck of the draw, especially with such a small sample size. I set out o see if there was on objective way to determine a ranking of the AIs. Cracking open my old statistics book, I found the formula for determining sample size based on population size, confidence level, and error of margin:

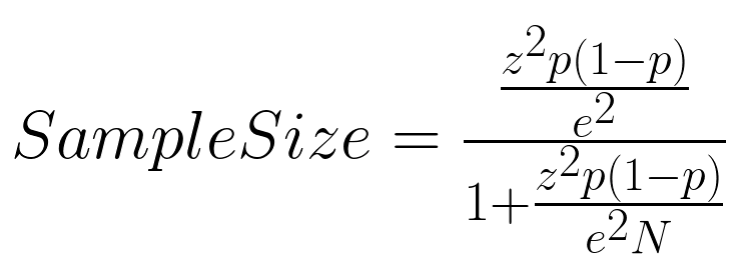
Our population size is the number of possible 10 card hands in a 52 card deck:

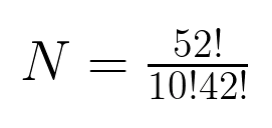
which is 15,820,024,220 different hands. With a confidence level of 95%, and an error of margin of 2%, we get a sample size of 2401 games. With that, I set out to play 48,020 games to get a better picture of how these AIs rank.

Here are the results:

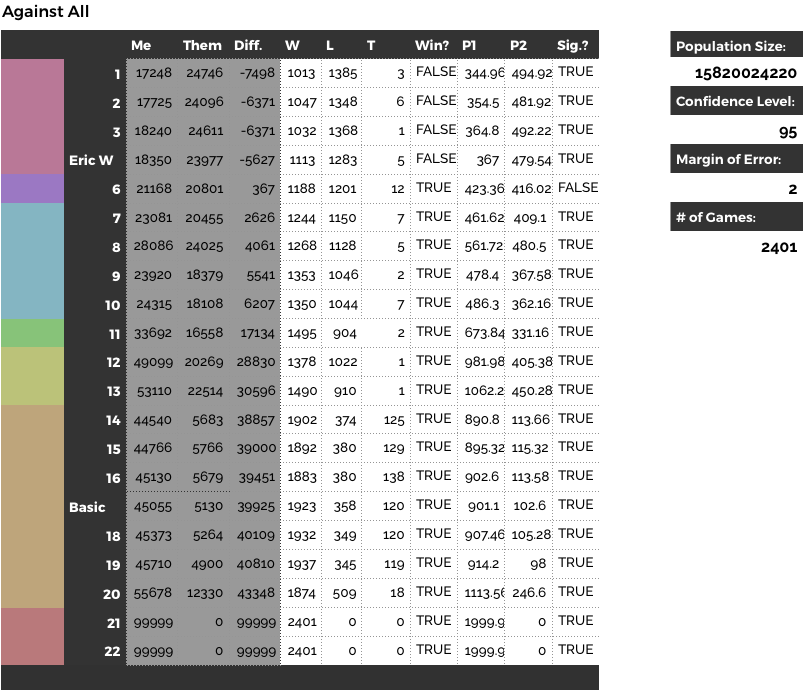
If you look at the ‘Win?’ column, I would be awarded 5th place. As you can see, there are 6 ‘ranks:’ red which is crashed, orange which is equivalent to my basic AI, yellow, green, and blue, purple - which was equivalent to me, and pink which was better than mine. Looking at the source codes of other classmates, it seems that orange is more or less my basic AI, yellow, green, and blue have different heuristics for choosing when to pick up discarded cards. The other purple is similar to mine, and the pink have different heuristics for determining what card to discard. What’s important to look at with this table is that these aren’t a singular order, there is a range with our margin of error.

And here is how those ranges look:

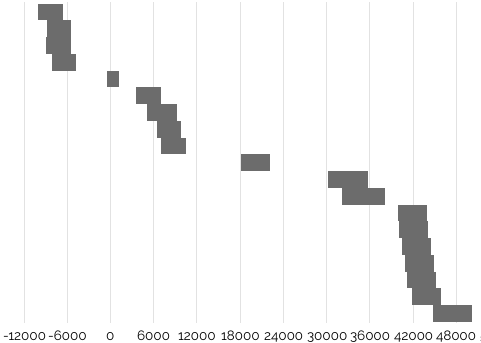
For any that overlap significantly, we can statistically say that they are of the same ranking, and the AIs in this ranking are equivalent. I would be number 5 according to this data, and in the second ‘ranking’ with one other classmate. It’s important to note, however, that this is only how these AIs perform against mine. In order for this to be completely statistically sound, I would have to pit each AI against every other AI, which would require me to run 456,190 games, which would be roughly 48 hours non-stop, not even including compiling all of the data. Maybe another time.

Aside from mass data collection (damn did this assignment make me feel like Verizon, I mean, I collected every card placed in the discard pile, every card pulled from the discard pile, who pulled it, how long ago they pulled it, how often they picked up from the deck, etc. etc. It felt dirty), the main logic of my AI boiled down to two simple decisions each turn: should I pick up from the discard pile, and what card should I discard? Those two decisions came down to these two methods, with some helpers:

bool ShouldDrawFromDiscardPile();
Card GetCardToDiscard();



private:

//returns true if the parameter completes
//    a set/run with our hand
    bool CheckForRunCompletion(Card card);
    bool CheckForSetCompletion(Card card);


//returns how many cards are part of a run from a given card,
//    on the left(lower) side, and right(higher) side
    int GetRightSideRunLength(Card card, std::vector<Card> sameSuit);
    int GetLeftSideRunLength (Card card, std::vector<Card> sameSuit);


//returns true if the supplied hand contains the card
    bool CheckIfCardIsInHand(Card card, Hand hand);


//returns the card that has the worst probability
//    of completing a set or run, given the number
//    of cards left in the deck, and the contents
//    of the discard pile in conjunction with what we
//    know of the other players' hands.
    Card FindWorstProbabilityLeft(std::vector<Card> cards);

Did I forget to mention that I fixed the looping bug? It came down to a very specific scenario: all four of a card needed to be in play, two of which player A has, one of which player B has, and the fourth is the top of the discard pile. Our (I say our because it affected a lot of us) AIs were incorrectly determining if a card completed a meld when choosing the discard pile. In this scenario, assume we have a 6Clubs, 6Hearts, 7Hearts, 8Hearts, and the top of the discard is a 6Spades. Our CheckForRunCompletion method sees that the 6S completes the 6 set, but it doesn’t see that the 6H is locked in the Hearts run. Our AI would then pick up the 6S, but when figuring out what card to discard, it would see the 6S and 6C as deadwood (because my AI prioritizes runs). Since it just picked up the 6S, it would discard the 6S. Assuming there is a similar situation on the opponent’s hand, it would discard the 6Diamonds, which then my AI would pick up. We would constantly loop, passing back these 6s. To fix this, we have to see if the discard card completes/extends a run, and if it does not, remove all the runs from the hand before checking if it completes/extends a set:

bool GinBrain::CheckForSetCompletion(Card card)
{
    //number of cards with the same value
	int numberOfCardsWithValue = 0;

	Card::Value value = card.getValue();

    //remove the runs from our hand
	Hand runLess = players.at(selfIndex)->GetHand();
	runLess.removeMatches(false);

    //find the cards with the same value, not counting the current card
	for (UINT i = 0; i < runLess.getNumCards(); i++)
	{
		Card c = runLess[i];
		if (c.getValue() == value && !(c == card)) numberOfCardsWithValue++;
	}

    //if there are two or more other cards with the same value, we have a set!
	return numberOfCardsWithValue >= 2;
}

With that fixed, I had a little bit of time to work on a heuristic for determining what card to discard. I don’t think it is as good as I hoped it would be, and I wish I had more time to implement it. I get all of the deadwood from my hand by removing all of the sets and runs, and then I go through the deadwood, finding the highest values, adding these to a vector. For each card in this vector, I then try to find the probability of the opponent picking it up, as well as the probability of it completing a set by looking to see how many of its value have already been discarded, and how many of the cards to the left and right of it (i.e. looking at QSpades, left and right cards are the JS and KS) have already been discarded. Based on this probability value, it discards the card that has the lower probability of forming a meld:

Card GinBrain::FindWorstProbabilityLeft(std::vector<Card> cards)
{
	Card returnCard;

	int worstProbability = -INT_MAX;

    //cards is the vector of highest value deadwood
	for (Card c : cards)
	{
		int probability = 0;

        //go through all the cards in the discard pile
		for (int i = 0; i < discardedCards.size(); i++)
		{
			Card discard = discardedCards[i];

            //check to see if this discarded card would help a run or set
			if (discard.getValue() == c.getValue() ||
	                   (discard.getSuit()  == c.getSuit() && abs(discard.getValue() - c.getValue() == 1)))
			{
                //if it does, add to the probability how close to the top of the discard pile it is
				probability += i;
			}
		}

        //go through all the known cards of all of the players
		for (int i = 0; i < players.size(); i++)
		{
            //RetrieveSurroundingCardsOf does what this method does, but resides in the Player class
			if (i != selfIndex && players[i]->RetrieveSurroundingCardsOf(c) >= 2)
			{
                //set probability to -1, we do not want to discard this card because the opponent will pick it up.
				probability = -1;
			}
		}

        //if we have a new worst card, set it
		if (probability >= worstProbability)
		{
			returnCard = c;
			worstProbability = probability;
		}
	}

	return returnCard;
}

  I think my weighting for the probability is broken, because logistically this heuristic should increase my win chances, but it seems to hamper them just enough to take me out of the top rank. If I had more time though, I would’ve spent more time on it. Oh well. I had fun with this assignment, it was very statistics-based like Minesweeper, but I’m really excited for our next, and final, assignment: Empire, a 1980s Civ-like exploration/kingdom game. I think it will be less math-heavy, and more mind games and sneaky tactics; I’m hoping it is at least.

Addendum: I forgot to mention, amongst all of this, I had a round of 100 games where my AI went 89-8-3 against my basic AI. A bit of an outlier, but still cool in its own right.