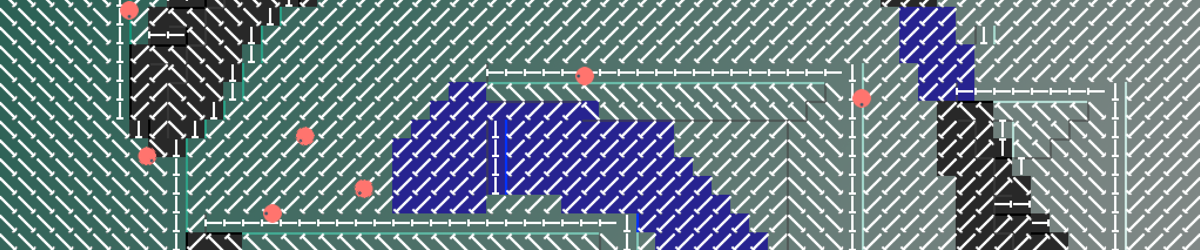
Flow Field Pathfinding

Flow fields are a form of pathfinding and are useful when handling many objects at once – like crowds, or hordes of enemies – because the paths are calculated all at once. In fact, all possible paths are calculated at once, using the terrain to calculate cost of movement. This project uses a tile-based approach to flow fields, and includes multiple types of terrain as well as an editor to test the functionality.

The Field

The flow field consists of three steps: creating a cost field based on the terrain, generating an integration field from the cost field based on the distance from the goal tile, and then creating the actual flow field using the values from the integration field.

The cost field is created by looking at the terrain at each tile. For instance, mountains would have a much higher cost value than a field, and water might be considered impassable depending on the game, giving it a humongous cost. These values are hard-coded into the game some how and are attached to each terrain.

The integration field is then calculated by using the cost of each tile, and adding to that the direct distance to the goal tile.

The integration field is where most of the work in the flow field calculation is done. In order to create the integration field we will use a modified version of Dijkstra’s algorithm.

This is a list of the steps that the algorithm takes to calculate the field:

• The algorithm starts by resetting the value of all cells to the max cost.
• The goal node then gets its total cost set to zero and gets added to the open list. From this point the goal node is treated like a normal node.
• The current node is made equal to the node at the beginning of the open list and gets removed from the list.
• All of the current node’s neighbors get their total cost set to the current node’s cost plus their cost read from the cost field. They then get added to the back of the open list. This happens if and only if the new calculated cost is lower than the old cost. If the neighbor is impassable, then it gets ignored completely.
• This algorithm continues until the open list is empty.

This gives higher cost tiles a higher integration number and gives a realistic cost of travel from a certain distance to the goal. From this integration field, the flow field is created. Each tile is given a direction of travel, and for this project was restricted to the 8 cardinal directions. This direction is found by looking at each tiles’ neighbors and finding the lowest cost amongst its neighbors. The direction of travel is towards the lowest cost neighbor.

void FlowFieldPathfinder::calculateFlowField()
{
	/*go through each cell and compare value to all of its
		neighbors to find the one with the lowest value.*/

	for (int i = 0; i < mpIntegrationField->getGridWidth() * mpIntegrationField->getGridHeight(); i++)
	{
		//Get the neighbors of the current node
		std::vector pNeighbors = mpIntegrationField->getAdjacentIndices(i);
		int neighborCount = pNeighbors.size();

		//find lowest neighbor
		int lowestNeighbor = 0;
		int lowestNeighborValue = 65535;
        	for (int j = 0; j < neighborCount; j++)
        	{
            		if (mpIntegrationField->getCostAtIndex(pNeighbors[j]) < lowestNeighborValue)
            		{
                		lowestNeighborValue = mpIntegrationField->getCostAtIndex(pNeighbors[j]);
               		 	lowestNeighbor = pNeighbors[j];
			}
		}

		//set direction to lowest neighbor
		unsigned short lowestX = lowestNeighbor % mpGrid->getGridWidth();
		unsigned short lowestY = lowestNeighbor / mpGrid->getGridWidth();

		unsigned short currentX = i % mpGrid->getGridWidth();
		unsigned short currentY = i / mpGrid->getGridWidth();


		Vector2D direction((lowestX - currentX) * 10.0f, (lowestY - currentY) * 10.0f);
		mpIntegrationField->setDirectionAtIndex(i, direction);
	}
}

This gives mountains a slope, and discourages travel across them, unless they are thin, or it costs less to go across than go around.

Retrospection and Postmortem

This project was created this past semester, so I feel a full retrospection wouldn’t be very beneficial. Regardless, I will say that the arrows for the visualization of the flow field are >3000 in count, and that could definitely be optimized, because for now the simulation slows down when the flow field is being visualized.

Flow fields are an interesting form of pathfinding because they are computationally expensive on the front end, but once calculated they can be used by any number of boids. This is good for static maps, or static goals, but if a map or path goal is constantly changing, this will not perform well. As such, games like TBS’s or RTS’s with static maps could be potential candidates for using flow fields to dictate their AI movement.